Почему две перпендикулярные прямые не пересекаются в геометрии 7 класса
1 минута чтение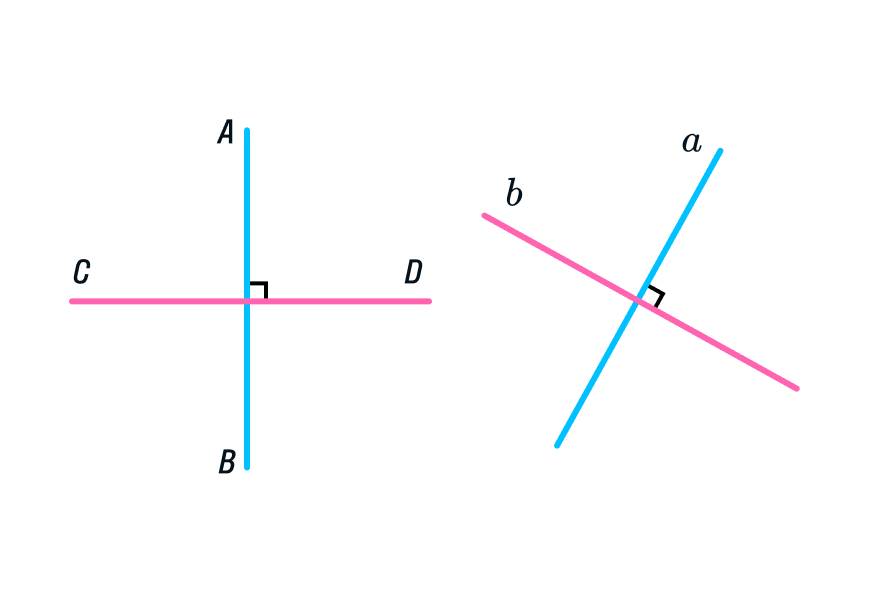
Геометрия — это наука, изучающая пространственные фигуры и их свойства. Один из основных концептов геометии — это прямая линия. Прямая линия может быть задана двумя точками или геометрическим определением, а также имеет свои характеристики, включая углы и пересечения.
Один из важных типов прямых — перпендикулярные прямые. Две прямые считаются перпендикулярными, если они пересекаются и образуют прямой угол в точке пересечения. Этот угол равен 90 градусам и является основой для изучения многих геометрических свойств.
Таким образом, по определению, две перпендикулярные прямые должны пересекаться. Однако, это не совсем верно. По фундаментальному принципу геометрии, две перпендикулярные прямые не могут пересекаться нигде, кроме своей точки пересечения. Это означает, что даже при продолжении прямых за их точку пересечения, они никогда не пересекутся в другой точке.
Законы геометрии в 7 классе
Законы геометрии в 7 классе включают, в том числе, и понятие перпендикуляра. Перпендикуляр- это прямая, которая образует прямой угол (равный 90 градусам) с другой прямой. Учиться анализировать перпендикулярные прямые и их свойства – одна из основных задач 7 класса в геометрии.
Одним из законов геометрии, которые учат в 7 классе, является закон о перпендикулярности. Согласно этому закону, если две прямые перпендикулярные третьей, то они параллельны между собой. И наоборот, если две прямые параллельные третьей, то они перпендикулярны друг другу.
Свойства перпендикулярных прямых позволяют решать разнообразные задачи в геометрии, включая построение перпендикуляров и нахождение углов между прямыми.
Общие понятия геометрии
Основные понятия геометрии включают:
- Точка: безразмерная, не имеющая ни длины, ни ширины объектная единица, которая используется для задания местоположения в пространстве. Точки могут быть заданы координатами или с помощью геометрической фигуры.
- Прямая: бесконечно длинная и бесконечно тонка линия, которая не имеет ширины и состоит из бесконечного числа точек. Прямая может быть задана двумя различными способами: с помощью двух точек или с помощью уравнения.
- Отрезок: часть прямой, ограниченная двумя точками. Отрезок имеет конечную длину и включает в себя все точки, которые лежат между его конечными точками.
- Угол: область плоскости, образованная двумя лучами, имеющими общее начало, называемым вершиной угла. Углы могут быть различных видов в зависимости от их величины и взаимного расположения лучей.
- Перпендикулярные прямые: две прямые, которые пересекаются под прямым углом и не лежат в одной плоскости. Перпендикулярные прямые могут служить основой для построения прямоугольников, квадратов и других геометрических фигур.
Понимание этих основных понятий геометрии является важным для изучения более сложных тем, таких как теоремы, связанные с углами, пересечением прямых и плоскостей, и многими другими.
Две перпендикулярные прямые
Перпендикулярные прямые имеют следующие свойства:
- Перпендикулярные прямые имеют равные прямоугольные углы, то есть каждый угол равен 90 градусам.
- Точка пересечения перпендикулярных прямых называется точкой пересечения или точкой прямоугольника.
- Перпендикулярные прямые не пересекаются нигде, кроме точки пересечения.
- Если прямая, проходящая через точку пересечения перпендикулярных прямых, разделена на две равные части, то каждая из этих частей является высотой прямоугольника.
Перпендикулярные прямые широко используются в строительстве, геодезии, архитектуре и других областях. Они помогают определить направления, углы и построить прямоугольные фигуры.
Знание о перпендикулярных прямых позволяет упростить решение задач и построение различных фигур. Поэтому понимание и умение работать с перпендикулярными прямыми является важным навыком в геометрии.
Доказательство: пересечение или параллельность?
Рассмотрим две перпендикулярные прямые. Чтобы понять, пересекаются ли они или параллельны, нам нужно провести некоторое доказательство.
Допустим, у нас есть перпендикулярные прямые l и m. Предположим, что они пересекаются в точке A. Если так, то у нас должны быть два прямолинейных угла: угол между прямыми l и m и угол между прямыми m и l. По определению перпендикулярных прямых, эти углы должны быть равными 90°.
Теперь рассмотрим точку A. Она лежит как на прямой l, так и на прямой m. Следовательно, она принадлежит обеим прямым одновременно. Но в то же время она является точкой пересечения прямых l и m. Это противоречие!
Из нашего доказательства следует, что две перпендикулярные прямые не могут пересекаться в одной точке, а следовательно, они параллельны.
Таким образом, перпендикулярные прямые всегда либо параллельны, либо не пересекаются вовсе.
Закон параллельности
Перпендикулярные прямые — это две прямые, которые пересекаются под прямым углом. По определению перпендикулярности, угол между двумя перпендикулярными прямыми равен 90 градусам. Таким образом, поскольку эти прямые образуют прямой угол, они никогда не пересекаются.
Закон параллельности используется для определения свойств квадратов, прямоугольников и других геометрических фигур. Например, если две прямые пересекаются под прямым углом, то это означает, что они перпендикулярны и лежат в одной плоскости. Это свойство используется для конструирования и измерения геометрических фигур и применяется в различных областях науки и техники.
Понимание закона параллельности позволяет ученикам лучше понять геометрические концепции и решать задачи, связанные с построением и измерением прямых и углов. При изучении геометрии 7 класса, важно запомнить, что перпендикулярные прямые не пересекаются и использовать этот принцип при решении задач.
Сущность закона параллельности
Существует несколько способов доказательства закона параллельности, однако все они основаны на аксиоме плоскости, которая утверждает, что через одну точку можно провести только одну прямую, параллельную другой прямой. Это означает, что если две прямые пересекаются, то они никак не могут быть параллельными.
Закон параллельности имеет широкое применение в различных областях науки и техники, особенно в геометрии и физике. Например, в архитектуре закон параллельности используется для создания симметричных и эстетически приятных строений. В физике закон параллельности помогает в решении задач, связанных с оптикой и светом.
В заключении, закон параллельности является важным принципом, который помогает понять и объяснить поведение прямых линий. Он позволяет предсказывать и анализировать геометрические свойства и взаимодействие прямых, что делает его важным элементом изучения геометрии в школе.
Примеры и применение в геометрических задачах
Концепция перпендикулярности играет важную роль в геометрии и находит широкое применение в различных геометрических задачах. Рассмотрим несколько примеров, где перпендикулярные прямые используются для решения задач.
1. Построение прямой, перпендикулярной данной прямой: для построения перпендикулярной прямой к данной прямой, необходимо взять точку на данной прямой в качестве центра и провести окружность, а затем провести две хорды окружности через эту точку, образуя прямые, перпендикулярные данной прямой.
2. Поиск высот в треугольнике: высота треугольника — это отрезок, проведенный из вершины до противоположной стороны, перпендикулярный этой стороне. Для нахождения высоты в треугольнике можно использовать свойство перпендикулярных прямых. Найдем прямую, проходящую через вершину треугольника и перпендикулярную одной из его сторон, а затем найдем точку пересечения этой прямой с противоположной стороной. Полученный отрезок будет являться высотой треугольника.
3. Построение прямоугольника: для построения прямоугольника можно использовать свойство перпендикулярных прямых. Найдем две перпендикулярные прямые, зная две точки и одну из сторон прямоугольника. Постройка осуществляется путем построения двух прямых, перпендикулярных данной стороне и проходящих через две заданные точки.
4. Построение касательной к окружности: чтобы построить касательную к окружности, необходимо провести прямую, перпендикулярную радиусу окружности, проходящую через точку касания. Перпендикулярность применяется для нахождения и построения данной прямой.
Все эти примеры наглядно демонстрируют, как перпендикулярные прямые могут быть использованы для решения геометрических задач различной сложности.
Доказательство перпендикулярности
Для доказательства перпендикулярности двух прямых необходимо использовать определение перпендикулярности и свойства прямых углов.
Определение перпендикулярности:
Две прямые называются перпендикулярными, если они пересекаются и образуют прямой угол друг с другом.
Доказательство:
Пусть у нас есть две прямые, которые пересекаются и образуют прямой угол. Обозначим их как линии AB и CD. Для доказательства перпендикулярности этих прямых, нам необходимо показать, что прямые AB и CD образуют прямой угол.
Шаг 1: Предположим, что у нас есть две пересекающиеся прямые AB и CD, и мы хотим доказать, что они перпендикулярны.
Шаг 2: Рассмотрим прямые углы, образованные этими прямыми. Прямой угол равен 90 градусов.
Шаг 3: Докажем, что прямые AB и CD образуют прямой угол. Это можно сделать, показав, что две пары углов, образованных пересекающимися прямыми, равны между собой.
Шаг 4: Рассмотрим углы, образованные AB и CD. У каждой пары углов будет по два угла: угол A и угол D, а также угол B и угол C.
Шаг 5: Докажем, что угол A равен углу D и угол B равен углу C. Это можно сделать, используя свойства параллельных прямых и свойств прямых углов.
Шаг 6: Поскольку прямые AB и CD пересекаются и образуют прямой угол, и углы A и D равны, а также углы B и C равны, то мы можем заключить, что прямые AB и CD перпендикулярны.
Заключение:
Таким образом, мы доказали перпендикулярность двух прямых AB и CD, поскольку они пересекаются и образуют прямой угол. Доказательство было основано на определении перпендикулярности и свойствах прямых углов.
Способы доказательства перпендикулярности
Один из способов — использование определения перпендикулярности. По определению, если две прямые перпендикулярны, то они образуют угол 90 градусов. Для доказательства можно провести углы и измерить их с помощью транспортира или использовать угловые измерения, предоставленные в условии задачи.
Другим способом является использование теоремы о перпендикулярных прямых. Согласно этой теореме, если существует прямая, перпендикулярная одной из них и проходящая через точку пересечения, то они перпендикулярны друг другу. Для доказательства можно провести дополнительную прямую и проверить, что она перпендикулярна и проходит через точку пересечения двух данных прямых.
Кроме того, можно использовать теорему о смежных углах. Если две прямые пересекаются, образуя при этом смежные углы равные между собой, то эти прямые являются перпендикулярными. Для доказательства можно измерить смежные углы или провести прямые, образующие эти углы, и проверить их равенство.
Таким образом, существует несколько способов доказательства перпендикулярности прямых, которые могут быть использованы в геометрии.
Вопрос-ответ:
Зачем нужно знать, почему две перпендикулярные прямые не пересекаются?
Знание этого свойства геометрических фигур поможет нам решать различные задачи и строить правильные построения.
Что такое перпендикулярные прямые?
Перпендикулярные прямые — это две прямые, которые образуют прямой угол в точке пересечения.
Почему перпендикулярные прямые формируют прямой угол?
Перпендикулярные прямые формируют прямой угол, потому что угол между ними равен 90 градусам.
Влияет ли расположение перпендикулярных прямых на то, пересекаются они или нет?
Нет, расположение перпендикулярных прямых не влияет на их пересечение, важно только, чтобы они образовывали прямой угол.



